Formulae & Assumptions

Dilute Binary Liquid Solutions

The thermal conductivity of liquids is calculated using Bridgman’s equation (BSL Eqn 9.4-3). This equation is limited to densities well above the critical density because of the assumption that each molecule oscillates in a “cage” formed by its nearest neighbors.

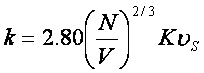
Here, N is Avogadro’s number, V is molar volume, K is Boltzmann’s constant, and u_s is sonic velocity. The Matlab program used to calculate thermal conductivity of liquids is klcalc.m.

It was also assumed that the thermal conductivity, density, viscosity, and heat capacity of the solution is equal to that of the solvent B because the solution is so dilute. In addition, the density of the solvent is independent of temperature. The Matlab program used to calculate liquid viscosity is liqmucalc.m.

Because of the unsatisfactory nature of the theory for diffusion in liquids, it is necessary to rely on empirical expressions. The Wilke-Chang equation (BSL Eqn 17.4-8) is used in this program and gives the diffusivity for small concentrations of solute A in solvent B as

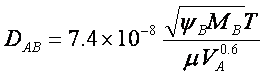
Here, V_A is the molar volume of the solute A at its normal boiling point, m is the viscosity of the solution, y_B is an “association parameter” for the solvent, M_B is the molecular weight of the solvent, and T is the absolute temperature.

Low Density Binary Gas Mixtures

Calculations involving low density gas mixtures operate on several core assumptions. First, low density implies ideal gases, and the ideal gas law was used to calculate the density of the mixture. In order to calculate the density of the mixture, an average molecular weight of the mixture was determined by weighing the mole fractions of the components with each pure component’s molecular weight. This was similarly performed for the heat capacity, and an average heat capacity was associated with the gas mixture.

The thermal conductivity for gas mixtures at low density may be estimated by BSL Eqn 9.3-17.

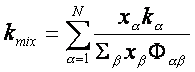
Here, x_a are the mole fractions, k_a are the thermal conductivities of the pure chemical species, and F_ab is a dimensionless quantity that is a function of the viscosities and molecular weights defined in BSL Eqn 1.4-16. The Matlab program used to calculate the thermal conductivity of gas mixtures is mixkt.m.

The binary diffusivity of low density gas mixtures is calculated using Chapman-Enskog kinetic theory. Approximating concentration using the ideal gas law, the empirical formula for diffusivity is expressed by BSL Eqn 17.3-12

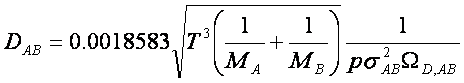
Here, T is temperature, M is the molecular weight of the component, p is pressure, s_AB is the characteristic diameter of the molecules called the collision diameter, and W_D,AB is a dimensionless quantity called the collision integral and is a function of dimensionless temperature. This value is associated with Lennard-Jones parameters, given by Table E.2 in BSL. The Matlab program used to calculate the diffusivity of gas mixtures is dcalc.m.